Rayleighův a Mieův rozptyl

	Modré nebe a bílé kumuly (foto Pavel Lahučký)

Když se řekne Rayleighův rozptyl, hodně lidí si jistě vybaví jeho souvislost s barvou oblohy. Ovšem Mieův rozptyl, který je obecnější než Rozptyl Rayleighův, již tak dobře znám není. A právě tento článek by vás měl seznámit blíže jak s Rayleighovým rozptylem, tak s rozptylem Mieovým. A jelikož je historie objevu zákonitostí Rayleighova rozptylu velmi spletitá a zajímavá, nebude určitě na škodu se u ní zdržet.
 
 

Zajímavá historie

Již odpradávna si lidé pokládají otázku proč že je vlastně obloha modrá. Jedna z prvních teorií, jež se snažily vysvětlit modrou barvu oblohy říká, že je tomu tak proto, že molekuly některého z plynů, které jsou ve vzduchu obsaženy, mají modrou barvu. K vyvrácení této teorie se stačí zamyslet nad tím, jak by asi vypadala okolní krajina, kdyby to byla pravda. Při pohledu do větší vzdálenosti bychom se totiž dívali přes silnou vrstvu vzduchu a vzdálenější předměty by se nám tudíž všechny musely jevit namodralé, podobně jako kdybychom se na ně dívali přes modře zbarvené sklo.

Další teorií, kterou vyvrátil Isaac Newton (1643 - 1727, anglický fyzik, matematik a astronom, který je znám především díky svým pohybovým zákonům, které jsou dodnes stěžejní součástí nebeské mechaniky a dalších odvětví fyziky) je, že modrá barva vzniká, smíchá-li se černá barva oblohy, která je v noci, s bílou barvou slunečních paprsků. Newton vyvrátil i předchozí teorii a dokázal tak, že vzduch není zabarven. I přes to se mu modrou barvu oblohy nepovedlo vysvětlit a kromě toho vytvořil další teorii, jež však byla opět scestná. Předpokládal totiž, že modrá barva oblohy vzniká stejným způsobem jako modrá část duhy, totiž lomem světla na dešťových kapkách. I když tato teorie měla vážné trhliny, tak ani takový vědec jako Newton, si jich nevšiml.

První správné krůčky k vysvětlení modré barvy oblohy podnikl až 200 let po Newtonovi Lord Rayleigh (John William Strutt, 3. baron Rayleigh [1842 - 1919], anglický fyzik, objevitel vzácného plynu argonu, držitel Nobelovy ceny za fyziku za rok 1904, kterou získal za zkoumání hustoty nejdůležitějších plynů a za objev argonu). Rayleigh se totiž zabýval mimo jiné výzkumem světla, které prováděl paradoxně v temné laboratoři. Je zcela pochopitelné, že paprskům světla se do cesty dostávala prachová zrnka, která byla tímto osvětlena. A právě tato prachová zrnka pravděpodobně přivedla Rayleigha na správnou cestu. Vyřkl proto teorii, že drobná prachová zrnka můžou mít na svědomí modrou barvu oblohy. Samozřejmě, že svou domněnku prověřil výpočtem. Roku 1871 tak vysvětlil, že drobná prachová zrníčka, jejichž velikost je menší než vlnová délka světla, mohou díky rozptylu zbarvovat oblohu do modra. K přesnějšímu fyzikálnímu vysvětlení se dostanu až později, ale dodám, že podobným způsobem vysvětlil i barvu červánků, modravý nádech z mlhy, načervenalou barvu slunce nízko nad obzorem a další podobné jevy.

Zdálo se, že problém zbarvení oblohy je vysvětlen, ovšem netrvalo dlouho a v teorii se objevily trhliny. Způsobují-li totiž modré zbarvení oblohy zrníčka prachu, musí být obloha ve městech, kde je prachu více, modřejší než obloha vysoko v horách. Pozorování však byla v protikladu s tímto závěrem a tak se Rayleigh pustil do ověřování svých rovnic. Shledal, že jsou správné z čehož vyplynulo, že "pachatelem" nejsou zrníčka prachu, ale musí jím být něco jiného. Rayleigh vzal v úvahu fakt, že čím je vzduch čistší, tím je barva oblohy modřejší a dospěl tak k závěru, že k rozptylu tedy musí docházet na molekulách, z nichž sestává vzduch.
 
Opět se zdálo, že tato teorie již zcela vysvětluje zbarvení oblohy, ale roku 1907 se znovu objevily otázky, který ji zpochybnily. Ruský fyzik Leonid Mandelštam (Leonid Isaakovič Mandelštam [1879 - 1944], sovětský fyzik, který se zabýval rozptylem světla, šířením rádiových vln, teorií nelineárních kmitů...) totiž poukázal na to, že počet molekul ve vzduchu je příliš velký (počet molekul v 1 m³; je roven N ~ cca 2,7 · 10²⁵. Při tak velkém počtu molekul se totiž vyruší složky rozptylu jdoucí do stran a světlo tak zachová pouze svůj původní směr. Mandelštam si však uvědomil, že molekuly vzduchu stejně jako molekuly každého plynu se pohybují. Jde o náhodný pohyb relativně velkými rychlostmi (například molekula kyslíku O₂ se při teplotě T = 273 K pohybuje střední rychlostí v = cca 650 m · s^-1. Při takovém náhodném pohybu nutně dochází k vzájemným srážkám a těsným přiblížením částic a tím pádem vznikají větší či menší shluky molekul, které se však zase rychle rozpadají. Velikost těchto shluků pak může o mnoho řádů přesáhnout velikost vlastních molekul. A právě tady tyto shluky mají na svědomí modrou barvu oblohy. Leonid Mandelštam byl tedy tím, kdo konečně dořešil tuto dlouholetou záhadu, ovšem nejvýznamnější měrou přispěl Rayleigh, a proto se rozptyl nazývá po něm.
 
Nedlouho poté pak uveřejnil Gustav Mie (Gustav Adolf Feodor Wilhelm Ludwig Mie [1869 - 1957], německý fyzik, jenž se roku 1908 zapsal do dějin fyziky ucelenou teorií rozptylu světla založenou na řešení Maxwellových rovnic) svou teorii rozptylu světla, která je obecnější než teorie Rayleighova.

Proč není obloha fialová?

Jaký je vlastně rozdíl mezi Rayleighovým a Mieovým rozptylem? Úplně jednoduše se dá říci, že Mieova teorie je obecnější teorií než Rayleighova; jinak řečeno Rayleighova teorie je podmnožinou Mieovy. Rayleighův rozptyl je omezen dvěma podmínkami:

1. musí být splněna relace 2 · p · r/l je mnohem menší než 1, kde r je poloměr rozptylující částice a l (lambda) je vlnová délka;
2. rozptylující částice musí být elektricky nevodivé.

Mieova teorie (někdy nazývaná též Lorenzova-Mieova teorie nebo Lorenzova-Mieova-Debyeova teorie) tato omezení nemá, a proto ji lze použít pro výpočet rozptylu na sférických částicích libovolné velikosti a pro částice elektricky nabité. Rozšířenou Mieovu teorii lze pak použít i pro výpočet rozptylu na nesférických částicích, čehož se využívá například v meteorologii při radiolokaci neboť ledové částice a velké kapky nemají obecně sférický tvar. Mieova teorie má však oproti Rayleighově jednu velkou nevýhodu. Tato plyne z její komplexnosti a tudíž je složitější. Proto v případě, že je splněna výše uvedená relace pro Rayleighův rozptyl, používá se právě teorie Rayleighova.
 
A jak velké vlastně částice musí být, aby byla tato teorie použitelná? Vezmeme-li v úvahu viditelné záření, které zaujímá rozmezí vlnových délek od l_min = 4,0 · 10^-7 m do l_max = 7,9 · 10^-7 m, pak lze podle následujícího spočíst zhruba velikost částic.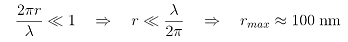
 


 
Maximální velikost částic, pro které lze použít Rayleighovu teorii, tak vychází
r_max = cca 1,0 · 10^-7 m. Ještě jednou upozorním na skutečnost, že jde o horní hranici velikosti částic a že Rayleighova teorie se lépe uplatní pro částice o řád a více řádů menších než je uvedená hodnota r_max.
 
Dalším důležitým poznatkem týkajícím se Rayleighova rozptylu je fakt, že intenzita tohoto rozptylu závisí nepřímo úměrně na čtvrté mocnině vlnové délky; I je úměrné 1/l⁴. Přesněji tuto skutečnost vystihuje vztah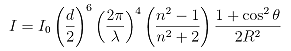
 
   (1)
 
kde I₀  je původní intenzita světla, d je průměr rozptylující částice, n je její index lomu, θ je rozptylový úhel a R je vzdálenost od částice. Tento vztah už je přímým vysvětlením faktu, proč je obloha modrá, ale než tuto skutečnost popíši slovně, ještě uvedu obrázek, kde je názorně vidět, jak rozptyl vypadá. Z obrázku 1 je vidět, že malé částice, pro které lze použít Rayleighovu teorii, rozptylují světlo do všech stran. I když se zpětný a dopředný rozptyl vyznačují poněkud vyšší intenzitou rozptýleného světla, tak i rozptyl do stran má nezanedbatelnou intenzitu. Pro větší částice pak začíná převládat dopředný rozptyl.

Obrázek 1: Rayleighův a Mieův rozptyl. Šipkou dole na obrázku je vyznačeno odkud přichází rozptylované záření.
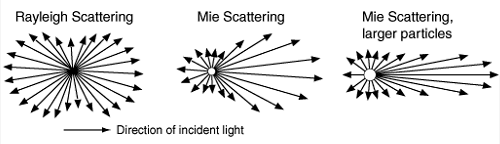
Obrázek převzat z http://hyperphysics.phy-astr.gsu.edu.
 
 
A nyní již k samotnému zbarvení oblohy. K tomu poslouží vztah (1). Jak známo, viditelné záření se skládá z jednotlivých barevných složek, které lze vidět při rozkladu světla. Toho lze dosáhnout buď pomocí hranolu nebo jiného optického zařízení. Stačí si však počkat na duhu nebo například cirkumzenitální oblouk, které jednotlivé barevné složky ukazují v celé své kráse.
 
Také je znám fakt, že červená část viditelného záření má největší vlnové délky (maximum u l_r = cca 640 nm a směrem k modré části viditelného záření vlnové délky klesají. Minima pak dosahují u fialové barvy, jejíž střed leží u hodnoty l_v = cca 430 nm. A jelikož velikost rozptylu závisí nepřímo úměrně na čtvrté mocnině vlnové délky (viz opět vztah (1)), je zřejmé, že fialová část viditelného záření se bude rozptylovat nejvíce a směrem k červené části bude velikost rozptylu velice rychle klesat.
 
Nyní už je docela pochopitelné, proč není obloha červená. Vyvstala však nová otázka. Má-li fialová barva kratší vlnovou délku než modrá, proč není obloha fialová? Ze vztahu (1) totiž plyne, že fialová se bude rozptylovat ještě více než modrá. K pochopení tohoto faktu poslouží obrázek 2.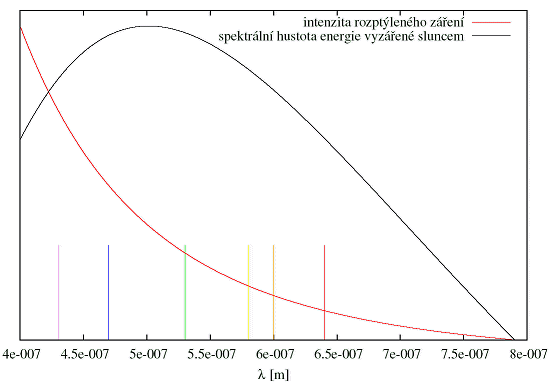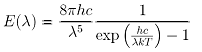
 

Obrázek 2: Relativní intenzita Rayleighova rozptylu v závislosti na vlnové délce.
  Na obrázku 2 je červenou čarou vyznačena velikost Rayleighova rozptylu v závislosti na vlnové délce. Černou křivkou (opět v relativní škále) je pak vyznačena spektrální hustota energie vyzářené sluncem, která udává, jaké množství záření připadá na danou vlnovou délku. Tvar této křivky byl spočten pomocí Planckova zákona pro absolutně černé těleso
 

 
kde h je Planckova konstanta, c je rychlost světla, l je vlnová délka, k je Boltzmannova konstanta a T je termodynamická teplota. V grafu jsou mimoto úsečkami v dolní části zaneseny typické vlnové délky pro jednotlivé barevné složky bílého světla (barevné složky jsou charakterizovány barvou čar). Již první pohled na graf naznačí, proč není obloha fialová. I když fialová barva podstupuje z viditelného záření největší rozptyl, je hustota energie jí přenášená menší než u modré barvy. Dalším důvodem je, že lidské oko je na fialovou část viditelného záření mnohem méně citlivé než na modrou. A konečně posledním faktem, který znevýhodňuje fialovou barvu je, že ve fialové barvě atmosféra propouští o něco méně záření než v modré, protože zde již pomalu končí atmosférické okno pro viditelné záření.

Roman Maňák
Článek vyšel původně ve zpravodaji Parhelium č. 3/2007

 
 
Přehled článků